Chapter 2 Neural networks
2.1 Neural networks as a regression model
2.1.1 Introduction
- Neural Networks are nonlinear regression models
- Underfitting: neural networks have higher capacity than linear models, with many (thousands or millions) parameters
- Overfitting: neural networks usually handle overfitting better than linear models, but
- nobody knows why,
- this is not always true, and
- overfitting is still a problem in neural networks
- Neural networks have a long history
- 1950s: models based on biological neurons
- 1960s: multilayer perceptron
- 1980s: backpropagation. Neural networks are omnipresent in academic research
- 2010s: deep learning. Neural networks are omnipresent
2.1.2 Artificial neurons
- Recall the linear regression model: \[ y=b+\sum_i x_i w_i \]
- It can be viewed as an input-output model:
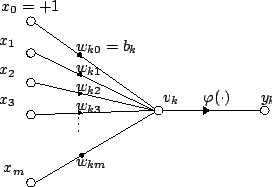
- If we post-process the output by a non-linear function \(\varphi\) then we have an artificial neuron: \(y=\varphi\left(b+\sum_i x_i w_i \right)\)
- The function \(f\) is the activation or transfer function
- Linear function: \(\varphi(z)=k\, z\)
- Sigmoid (logistic) function: \(\varphi(z)=\frac{1}{1+e^{-z}}\)
- Softmax function (for multiple outputs)
- Rectified linear units (ReLU): \(\varphi(z)=\max(0,z)\)
2.1.3 Artificial neural networks
- A neural network is composed by many neurons arranged in layers
- There is an input layer: \(y^1=x\)
- Outputs of neurons \(y^l\) at layer \(l\) (hidden layers) are the inputs of all neurons at the next layer \(l+1\)
- The output of the network \(\hat{y}\) is the output of the neuron \(y^N\) at the last layer \(L\) (output layer)
- Connections are one-directional: there are no loops
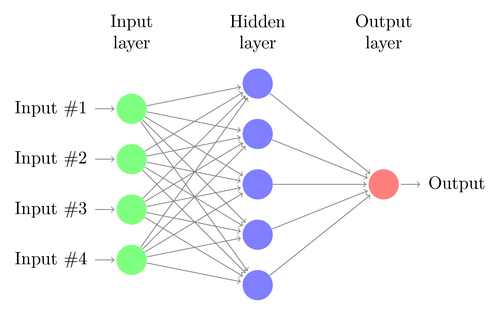
- All neurons include a bias or intercept, that can be thought of as a neuron with output fixed to 1 (not shown in the figure)
- Computation proceeds in feed-forward direction, layer by layer
\[\begin{aligned} y^0&=x \\ y^1&=\varphi\left(b^{1}+W^1\,y^{0}\right)\\ \dots&=\dots \\ y^l&=\varphi\left(b^{l}+W^l\,y^{l-1}\right) \\ \dots&=\dots \\ \hat{y}&=y^{L} \end{aligned}\]
2.1.4 Neural Networks in R
- There are many packages for neural networks, see a comparison
- We will use nnet (for now)
- Using nnet is very similar to lm: it uses the same formula syntax y ~ x
- For using nnet we have to set the size of the hidden layer
2.1.5 Design of a neural network
- Network design = setting hyper-parameters
- We have to set the number of layers
- We have to set the number of neurons at each hidden layer
- The input layer must match the number of inputs or regressors
- The output layer has one neuron for regression
- We have to set the activation functions
- Usually sigmoid in hidden layers
- At the output layer, it must match the possible outputs:
- Sigmoid functions are bounded
- Use linear output to allow arbitrary large outputs
- Sigmoid functions can be used if data is normalized
- Network fitting: the computational cost depends on the network size
- Computation of layer \(l\): \(y^l=\varphi\left(b^{l}+W^l\,y^{l-1}\right)\)
- The matrix \(W^l\) has dimensions \(N_l \times N_{l-1}\) where \(N_l\) is the number of neurons of layer \(l\)
- There are \(N_l \times (N_{l-1}+1)\) parameters to be learned at layer \(l\)
- Evaluate errors
- The concepts of training error and test error are as important as in linear regression (or more)
- The error is only computed at the output layer: \[ E_{\{x,y\}}(b^1,W^1,\dots,b^L,W^L) = \|y-\hat{y}\|^2 \]
- But the error depends on parameters at all layers
2.1.6 Examples
- Compare graphically the fit produced by a neural network (size=10) and a linear model. We will talk about maxit in next class, for now just try that nnet finishes with the message converged
data("cars")
# Hyperparameters
# One hidden layer, ten units: size=10
# What happens if we don't use linout=FALSE??
# We will talk about maxit in next class
modelo_neuronal = nnet(dist ~ speed, data=cars, size=10, linout=TRUE, maxit=1000)
with(cars, plot(speed, dist))
modelo_lineal = lm(dist ~ speed, data=cars)
lines(cars$speed, predict(modelo_lineal), col="red")
lines(cars$speed, predict(modelo_neuronal), col="green")- Analyse the fitting
data("cars")
# Hyperparameters
# One hidden layer, ten units: size=10
modelo_lineal = lm(dist ~ speed, data=cars)
modelo_neuronal = nnet(dist ~ speed, data=cars, size=10, linout=TRUE, maxit=1000)
summary(modelo_neuronal)- Compute the errors
# WARNING: This is only an example. In practice always partition training/test
data("cars")
# Hyperparameters
# One hidden layer, ten units: size=10
modelo_lineal = lm(dist ~ speed, data=cars)
modelo_neuronal = nnet(dist ~ speed, data=cars, size=10, linout=TRUE, maxit=1000)
cat("Error RMS modelo lineal = ", sqrt(sum(modelo_lineal$residuals^2) / nrow(cars)), "\n")
cat("Error RMS red neuronal = ", sqrt(sum(modelo_neuronal$residuals^2) / nrow(cars)), "\n")Results are not deterministic
Try normalization (linout=FALSE)
# WARNING: This is only an example. In practice always partition training/test
data("cars")
cars$norm_dist = cars$dist / max(cars$dist)
# Hyperparameters
# One hidden layer, ten units: size=10
modelo_lineal = lm(norm_dist ~ speed, data=cars)
modelo_neuronal = nnet(norm_dist ~ speed, data=cars, size=10, maxit=1000)
cat("Error RMS modelo lineal = ", sqrt(sum(modelo_lineal$residuals^2) / nrow(cars)), "\n")
cat("Error RMS red neuronal = ", sqrt(sum(modelo_neuronal$residuals^2) / nrow(cars)), "\n")- Always check training and test errors
data("mtcars")
# For sample.split
library(caTools)
# Partition data
indices = sample.split(mtcars$mpg)
mtcars_train = mtcars[indices,]
mtcars_test = mtcars[! indices,]
# Fit the models
modelo_1 = lm(mpg ~ disp + drat + wt, data=mtcars_train)
modelo_2 = nnet(mpg ~ disp + drat + wt, data=mtcars_train, size=100, linout=TRUE, maxit=1000)
# Check errors
cat("Training error (linear model):", sqrt(sum(modelo_1$residuals^2) / nrow(mtcars_train)), "\n")
prediction_1 = predict(modelo_1, newdata=mtcars_test)
error_test_1 = sqrt(sum((mtcars_test$mpg - prediction_1)^2) / nrow(mtcars_test))
cat("Test error (linear model):", error_test_1, "\n")
cat("Training error (neural network):", sqrt(sum(modelo_2$residuals^2) / nrow(mtcars_train)), "\n")
prediction_2 = predict(modelo_2, newdata=mtcars_test)
error_test_2 = sqrt(sum((mtcars_test$mpg - prediction_2)^2) / nrow(mtcars_test))
cat("Test error (neural network):", error_test_2, "\n")- Check different network sizes (it will probably require MaxNWts and adjusting maxit)
# Try changing network size
data("mtcars")
# Partition data
indices = sample.split(mtcars$mpg)
mtcars_train = mtcars[indices,]
mtcars_test = mtcars[! indices,]
# Fit the models
modelo_1 = lm(mpg ~ disp + drat + wt, data=mtcars_train)
modelo_2 = nnet(mpg ~ disp + drat + wt, data=mtcars_train, size=1000, linout=TRUE, MaxNWts=10000, maxit=1000)
# Check errors
cat("Training error (linear model):", sqrt(sum(modelo_1$residuals^2) / nrow(mtcars_train)), "\n")
prediction_1 = predict(modelo_1, newdata=mtcars_test)
error_test_1 = sqrt(sum((mtcars_test$mpg - prediction_1)^2) / nrow(mtcars_test))
cat("Test error (linear model):", error_test_1, "\n")
cat("Training error (neural network):", sqrt(sum(modelo_2$residuals^2) / nrow(mtcars_train)), "\n")
prediction_2 = predict(modelo_2, newdata=mtcars_test)
error_test_2 = sqrt(sum((mtcars_test$mpg - prediction_2)^2) / nrow(mtcars_test))
cat("Test error (neural network):", error_test_2, "\n")2.2 Backpropagation learning
2.2.1 Training error in neural networks
- Recall the general loop of learning techniques:
- Define a family of parameterized models
- Fit the model by computing the optimal parameters
- Check the errors
- The output of neural networks results from feed-forward computation by layers:
\[\begin{aligned} y^0&=x \\ y^1&=\varphi\left(b^{1}+W^1\,y^{0}\right)\\ \dots&=\dots \\ y^l&=\varphi\left(b^{l}+W^l\,y^{l-1}\right) \\ \dots&=\dots \\ \hat{y}&=y^{L} \end{aligned}\]
- The training error is a very complex function of all parameters: \(E=\sum_{i=1}^n (y_i-\hat {y_i})^2\)
2.2.2 Error minimization in neural networks
- The minimization problem \(\min_W E\) has no direct solution: we need numerical algorithms
- The basic idea of most numerical optimization methods is gradient descent: \(w_{ij}^l(t) = w_{ij}^l(t-1)- \alpha \, \nabla E(w_{ij}^l(t-1))\)
- The hyperparameter \(\alpha\) is called learning rate
- Numerical methods (mostly) are iterative algorithms. They require:
- Initialization
- Step adjustment
- Convergence check
- Historical note: gradient computation in neural networks was called backpropagation
2.2.3 Gradient descent in R
- The package nnet uses an automatic gradient preconditioning (BFGS), it does not need setting \(\alpha\)
- Increase maxit if the network does not converge
- Check the evolution of the error during execution (trace=TRUE)
- We can manipulate the stop condition (be careful):
- \(E< abstol\)
- \(E_{n+1}-E_n \ge (1-reltol)\)
- Weight initialization: random in \([-rang,rang]\)
# Try changing network size
data("mtcars")
# Partition data
indices = sample.split(mtcars$mpg)
mtcars_train = mtcars[indices,]
mtcars_test = mtcars[! indices,]
# Fit the models
modelo_1 = lm(mpg ~ disp + drat + wt, data=mtcars_train)
modelo_2 = nnet(mpg ~ disp + drat + wt, data=mtcars_train, size=100, linout=TRUE, MaxNWts=10000, maxit=1000)
# Check errors
cat("Training error (linear model):", sqrt(sum(modelo_1$residuals^2) / nrow(mtcars_train)), "\n")
prediction_1 = predict(modelo_1, newdata=mtcars_test)
error_test_1 = sqrt(sum((mtcars_test$mpg - prediction_1)^2) / nrow(mtcars_test))
cat("Test error (linear model):", error_test_1, "\n")
cat("Training error (neural network):", sqrt(sum(modelo_2$residuals^2) / nrow(mtcars_train)), "\n")
prediction_2 = predict(modelo_2, newdata=mtcars_test)
error_test_2 = sqrt(sum((mtcars_test$mpg - prediction_2)^2) / nrow(mtcars_test))
cat("Test error (neural network):", error_test_2, "\n")- For deterministic experiments, set the initial weights (Wts)
n_pesos = length(modelo_2$wts)
pesos = runif(n_pesos, min=-0.7, 0.7)
for (i in (1:10)) {
modelo_determ = nnet(mpg ~ disp + drat + wt, data=mtcars_train, size=100, linout=TRUE, MaxNWts=10000, maxit=1000, Wts=pesos, trace=FALSE)
print(sqrt(sum(modelo_determ$residuals^2) / nrow(mtcars)))
}- Output can be multidimensional
- This is more efficient than two separate regressions, because weights in the hidden layers are shared
- Warning: this is a long execution
- Data for this code
# Database loaded externally
# https://www.kaggle.com/datasets/elikplim/eergy-efficiency-dataset
library(readr)
library(caTools)
library(nnet)
datos = read_csv("ENB2012_data.csv")
# Partition data
indices = sample.split(cbind(datos$Y1))
datos_train = datos[indices,]
datos_test = datos[! indices,]
# Fit the models
X = datos_train[, 1:8]
Y = datos_train[, 9:10]
t0 = Sys.time()
modelo_md = nnet(X, Y, size=300, linout=TRUE, MaxNWts=100000, maxit=5000)
tf = Sys.time()
print(tf -t0)
# Check errors
cat("Training error (neural network):", sqrt(sum(modelo_md$residuals^2) / nrow(datos_train)), "\n")
X_test = datos_test[, 1:8]
Y_test = datos_test[, 9:10]
prediction = predict(modelo_md, newdata=X_test)
error_test = sqrt(sum((Y_test - prediction)^2) / nrow(datos_test))
cat("Test error (neural network):", error_test, "\n")
# Always have linear regression as base line
modelo_lin = lm(Y1 ~ X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8, data=datos_train)
# This is only Y1 (it is not comparable!!)
cat("Training error (linear model):", sqrt(sum(modelo_lin$residuals^2) / nrow(datos_train)), "\n")
prediction_lin = predict(modelo_lin, newdata=datos_test)
error_test_lin = sqrt(sum((datos_test$Y1 - prediction_lin)^2) / nrow(datos_test))
cat("Test error (linear model):", error_test_lin, "\n")- Observe the very slow error decreasing
iter 900 value 1609.212529
iter 910 value 1608.937640
iter 920 value 1608.811216
iter 930 value 1608.745116
iter 940 value 1608.636313
iter 950 value 1608.473398
iter 960 value 1608.328241
iter 970 value 1608.193417
iter 980 value 1608.122278
iter 990 value 1608.036335
iter1000 value 1607.998032
final value 1607.998032
stopped after 1000 iterations
Training error (neural network): 1.730436
Test error (neural network): 2.739645 2.3 Regularization
- Recall the critical concept of capacity:
- Too few parameters: large training error (underfitting)
- Too many parameters: large test error (overfitting)
- Regularization techniques are methods to avoid overfitting without losing (much) capacity
2.3.1 Ridge regression
- Linear regression can be expanded by including polynomial terms
- Problem of high-order polynomial models: very large parameters (NA)
- We can penalize large parameters in the optimization: \(E=\|y-\hat{y}\|^2+\lambda\, \|\theta\|^2\)
- The optimization problem is still LIP (Linear In the Parameters)
- Including the norm of the parameters in the target function is called:
- Tikhonov regularization (or L2 regularization)
- Ridge regression (when applied to linear regression)
- We can use ridge regression in R with the package glmnet
# Ohm's law is an empirical law
# number of samples
n_samples = 100
# Voltage (volts) (sort only for plotting)
voltage = runif(n_samples, min=50, max=100)
voltage = sort(voltage)
# Resistance (ohms)
resistance = 50
# "Measure" current
current = voltage / resistance
# Add noise
noise = runif(n_samples, min=0.8, 1.2)
current = current * noise
# Build a data frame
measures = data.frame(voltage, current)
# Compute polynomial terms
degree = 7
for (i in 2:degree) {
measures = cbind(measures, voltage^i / max(voltage^i))
colnames(measures)[i+1] = paste("voltage", i, sep="")
}
# Stadardize data
measures = as.data.frame(scale(measures))
# Fit a polynomial model
modelo_poly = lm(current ~ ., data=measures)
# Add regularization
measures_x = as.matrix(measures[, -2])
measures_y = as.matrix(measures$current)
# Find the best lambda
modelo_cv = cv.glmnet(measures_x, measures_y, alpha=0)
lambda_best = modelo_cv$lambda.min
# Fit the final model
modelo_reg = glmnet(measures_x, measures_y, alpha=0, lambda=lambda_best)
# Print coefficients
cat("Máximo coeficiente:", max(modelo_poly$coefficients), "\n")
cat("Máximo coeficiente (regulariz.):", max(coef(modelo_reg)), "\n")
cat("Error:", sqrt(sum(modelo_poly$residuals^2) / nrow(measures)), "\n")
prediction = predict(modelo_reg, newx=measures_x)
error_reg = sqrt(sum((prediction - measures_y)^2) / nrow(measures))
cat("Error (regulariz.):", error_reg, "\n")2.3.2 Math recall: algebraic regularization
- Recall the least squares solution of linear regression: \(\theta^*=(X^\top X)^{-1}\,X^\top\,y\)
- The matrix \((X^\top X)^{-1}\) is singular
- If there are linearly dependent rows in \(X\)
- If there are more columns than rows in \(X\)
- The matrix \((X^\top X)^{-1}\) may be ill-conditioned: \(det(X^\top X)\approx 0\)
- If there are many columns in \(X\)
- If there are few rows in \(X\)
- The solution of \(\nabla E=0\) with regularization is \(\theta^*=(X^\top X+\lambda\,I)^{-1}\,X^\top\,y\)
- The matrix \((X^\top X)^{-1}+\lambda\,I\) is always positive-definite for \(\lambda>0\)
2.3.3 Weight decay
- Tikhonov regularization can allo be applied in neural networks: \(E=\|y-\hat{y}\|^2+\lambda\, \|W\|^2\)
- The standard gradient descent: \(w_{t+1} = w_{t} - \alpha \, \dfrac{\partial E}{\partial w}\)
- Regularization adds a term to the gradient: \(w_{t+1} = w_{t} - \alpha \, \dfrac{\partial E}{\partial w} -\lambda w_t\)
library(nnet)
# For sample.split
library(caTools)
# Try changing weight decay
data("mtcars")
# Partition data
indices = sample.split(mtcars$mpg)
mtcars_train = mtcars[indices,]
mtcars_test = mtcars[! indices,]
# Set hyperparameter grid
decay_values = c(0, 1e-4)
# Fit the models
for (i in 1:length(decay_values)) {
cat("Decay: ", decay_values[i], '\n')
modelo = nnet(mpg ~ disp + drat + wt, data=mtcars_train, size=500, linout=TRUE, MaxNWts=10000, maxit=1000, decay=decay_values[i], trace=FALSE)
# Check error
cat("Training error:", sqrt(sum(modelo$residuals^2) / nrow(mtcars_train)), "\n")
prediction = predict(modelo, newdata=mtcars_test)
error_test = sqrt(sum((mtcars_test$mpg - prediction)^2) / nrow(mtcars_test))
cat("Test error:", error_test, "\n")
cat("Max coefficient:", max(modelo$wts), "\n")
}Decay: 0
Training error: 0.2020726
Test error: 177.1406
Max coefficient: 58.74598
Decay: 1e-04
Training error: 0.2020858
Test error: 11.01574
Max coefficient: 10.88843 - The amount of regularization is related to the bias-variance tradeoff
- This is very long simulation: see results
library(nnet)
# For sample.split
library(caTools)
data("mtcars")
# Partition data
indices = sample.split(mtcars$mpg)
mtcars_train = mtcars[indices,]
mtcars_test = mtcars[! indices,]
# Set hyperparameter grid
decay_values = c(0, 1e-4)
n_tests = 100
errors_train = matrix(0, length(decay_values), n_tests)
errors_test = matrix(0, length(decay_values), n_tests)
# Fit the models
for (i in 1:length(decay_values)) {
for (j in 1:n_tests) {
cat("Iteration: ", i, j, "\n")
modelo = nnet(mpg ~ disp + drat + wt, data=mtcars_train, size=500, linout=TRUE, MaxNWts=10000, maxit=1000, decay=decay_values[i], trace=FALSE)
errors_train[i, j] = sqrt(sum(modelo$residuals^2) / nrow(mtcars_train))
prediction = predict(modelo, newdata=mtcars_test)
errors_test[i, j] = sqrt(sum((mtcars_test$mpg - prediction)^2) / nrow(mtcars_test))
}
}
save(errors_train, errors_test, file="errors_decay.Rdata")2.3.4 Implicit regularization
- Cross-validation: check test error and adjust the model hyper-parameters
- Early stopping: stop gradient descent before convergence
- Completely optimize training error = overfitting
- In nnet this can be done with maxit or reltol
2.3.5 A (big) data approach to regularization
- In linear regression, the model matrix \(X\) is ill-conditioned when it has many columns and few rows
- To avoid overfitting we could:
- Reduce variables: dimensionality reduction
- Create data instances: data augmentation
- We need big amounts of data (that are useless if quality is low)
2.3.6 Exercises
- Download some of the examples from Kaggle or UCI
- Build neural networks and choose the size
- For the same network size, try different values for the parameter decay
- Check training and test errors
- Set an extremely high value (e.g. decay=100) and see what happens to the error and the parameters
2.4 Classification
- In regression tasks, we aim at learning a numeric result: given data X, provide the value \(\hat{y}\)
- In classification tasks, we aim at learning a decision rule: given data X, y belongs to class C_i
2.4.1 Qualitative variables
- Qualitative variables can only take one of a finite number of values: \(x_i\in\{C_1,\dots C_k\}\)
- This is in contrast to (real) numeric values
- They can also be called:
- Categorical
- Discrete, in contrast to continuous
- In R, factors
- Each of the possible values \(C_j\) can be called:
- Levels
- Classes
- Categories
- Example: dataset mtcars
[, 8] vs Engine (0 = V-shaped, 1 = straight)
[, 9] am Transmission (0 = automatic, 1 = manual)
[,10] gear Number of forward gears- Qualitative variables must be numerically coded to be used by computational techniques
- Numerical codes have an intrinsic order that may not agree with that of the qualitativa variable
- Even if a discrete variable has a numeric meaning, the proportionality may not be respected
- Coding binary variables as {0,1} can be interpreted as probabilities
- When there are \(k>2\) levels, we can use binary coding on \(k\) binary class indicators
# We interpret an input variable (cylinders) as a factor
data("mtcars")
mtcars$cyl_factor = as.factor(mtcars$cyl)
# Fit the models
library(nnet)
modelo_num = nnet(mpg ~ cyl + disp + wt, data=mtcars_train, size=100, linout=TRUE, MaxNWts=10000, maxit=1000)
modelo_fac = nnet(mpg ~ cyl_factor + disp + wt, data=mtcars_train, size=100, linout=TRUE, MaxNWts=10000, maxit=1000)
# Compute number of parameters
cat("Coef names (cyl numeric):", modelo_num$coefnames, "\n")
cat("Parameters (cyl numeric):", length(modelo_num$conn), "\n")
cat("Coef names (cyl factor):", modelo_fac$coefnames, "\n")
cat("Parameters (cyl factor):", length(modelo_fac$conn), "\n")2.4.2 Methods for classification
- In classification, the output variable is categorical
- There are many methods for classification:
- Regression as a decision boundary
- Linear coefficients: logistic regression (glm in R)
- Neural networks
- Decision trees
- Random forests
- Support Vector Machines
- k-Nearest Neighbours
- etc.
- Regression as a decision boundary
- There are many examples in medicine, engineering, economics…
- Differential diagnosis
- Credit scoring
- Spam detection
- Failure prediction
- Recognition of hand-written digits

2.4.3 Classification with regression neural networks
- An output qualitative variable can be numerically coded
- After coding the qualitative variable, we build a regression model \(\hat{y}=F(x)\)
- For a qualitative variable, what is the meaning of \(\hat{y}=0.3\)?
- For binary (two-class) classification, predictions can be interpreted as probabilities, leading to a decision boundary:
\[\hat{y}=\begin{cases} 0 & \text{if } F(x) \le \frac{1}{2} \\ 1 & \text{if } F(x) > \frac{1}{2} \end{cases} \]
- In R, the class indicators are created automatically by nnet
# Classification with nnet
library(nnet)
library(caTools)
data(iris)
# Partition data
indices = sample.split(iris$Species)
datos_train = iris[indices,]
datos_test = iris[! indices,]
# Build and fit the model
modelo = nnet(Species ~ ., data=datos_train, size = 100)
# Check training error
cat("Training error:", sqrt(sum(modelo$residuals^2) / nrow(iris)), "\n")2.4.4 Class prediction from regression
- What is the meaning of a prediction \(\hat{y}\ne 0,1\)?
- Predictions can be interpreted as probabilities
- Do not forget to use sigmoid activation functions in the output layer (linout=FALSE)
2.4.5 Regression and classification errors
- The final aim is predicting discrete classes
- The numeric error is not meaningful
- It is more illustrative to check the classification error by looking at the confusion matrix
- In some applications, some errors are more important than others, e.g. false positives vs. false negatives in medicine
# Classification with nnet
library(nnet)
data(iris)
# Partition data
indices = sample.split(iris$Species)
datos_train = iris[indices,]
datos_test = iris[! indices,]
# Build and fit the model
modelo = nnet(Species ~ ., data=datos_train, size = 100)
# Check the classification error
print("Training error")
output = predict(modelo, type="class")
conf_mat_train = table(datos_train$Species, output)
print(conf_mat_train)
print("Test error")
prediction = predict(modelo, datos_test, type="class")
conf_mat_test = table(datos_test$Species, prediction)
print(conf_mat_test)- Accuracy can be obtained from the confusion matrix M: \(\text{accuracy}=\frac{trace(M)}{n}\)
- More detailed analysis has been developed for binary classification when we identify a class as positive, for instance, in medical diagnosis:
- True Positives (TP)
- True Negatives (TN)
- False Positives (FP)
- False Negatives (FN)
- \(\text{accuracy}=\frac{TP + TN}{n}\)
- \(\text{precision}=\frac{TP}{TP + FP}\)
- \(\text{recall}=\frac{TP}{TP + FN}\)
- \(\text{F}_1 = \frac{2\, TP}{2\, TP + FP + FN}\)
| prediction | ||
|---|---|---|
| Positive | Negative | |
| Positive | TP | FN |
| Negative | FP | TN |
2.5 Assignment
- Regression with Neural Networks
- Select a real-world problem (it may be the same as in the linear regression assignment)
- Build a neural network for regression
- Check training and test errors and compare with the linear model
- Repeat the learning process changing hyper-parameters
- Two or three values of size
- Two or three values of weight decay
- Make a two-way table with errors for all the hyper-parameter combinations
- Classification with Neural Networks.
- Select a real-world problem (or build an artificial example)
- Build a neural network for classification
- Show the confusion matrix