Chapter 3 Unsupervised learning and time series

3.1 Clustering

3.1.1 Unsupervised learning

Regression / classification
- Learns from a dataset that includes both input $X$ and output $y$
- Implies building an input-output model $y=F(X)$
- Constructs a model that does prediction $\hat{y}$
Unsupervised learning
- We only have input data $X$
- There is no value (regression) or label (classification) for output $y$
- There is no prediction $\hat{y}$
- Aims at finding information about the data
Typical tasks in unsupervised learning
- Clustering: reducing rows
- Dimensionality reduction: reducing columns
- Generative networks
Typical applications in unsupervised learning
- Preprocessing before classification / regression
- Blind Source Separation
- Descriptive statistics
  - Market segmentation
  - Recommender systems
  - Social network analysis
  - Anomaly detection
- Visualization

3.1.2 Clustering

Data is partitioned into several distinct groups
Instances within each group are quite similar to each other
Instances in different groups are well separated
Clustering aims at revealing a natural classification of data

In mathematical terms, in clustering

We have data $X=\{x_1,\dots x_n\},x_i \in \mathbb{R}^m$
We look for a partition into groups or clusters $C_1,\dots C_k$
- Each data point is assigned to a cluster $x_i\in C_j$
- Clusters are disjoint $C_j\cap C_l=\emptyset$
- Clusters include all data $\cup_j C_j=X$
Usually the number of clusters is much smaller than the original number of rows $k\ll n$

3.1.3 The $k$-means algorithm

The number of clusters $k$ is an hyperparameter that must be set
The algorithm computes $k$ cluster centroids $\mu_1,\dots \mu_k\in \mathbb{R}^m$
Each data instance is assigned to the nearest centroid
The $k$-means algorithm is an optimization problem $\min_{\mu_i} \frac{1}{n}\|x_i-\mu_{A(i))}\|^2$
- The $i$-th data instance is assigned to cluster $A(i)$
- The centroid of cluster $A(i)$ is $\mu_{A(i)}$

$k$-means is an iterative algorithm

Initialize centroids
Repeat until there is no change
1. Assign each data instance to the closest centroid: $A(i)=\min_j \|x_i-\mu_j\|$.
2. Compute centroids as the average of the points that belong to its cluster: $\mu_j=\frac{1}{|C_j|} \sum_{x_i\in C_j} x_i$

$k$-means is an example of EM (Expectation-Maximization) algorithm:

Assign each data instance to the closest centroid: Maximization of fitness (or minimization of error)
Move the centroid to the center of mass, which gives minimum average distance: Expectation

3.1.4 Example

k-means in R is computed with the command kmeans
Consider as an example the iris database without the species variable.

datos = iris[, 1:4]   # Numerical data !!!
n_clusters = 2
clustering = kmeans(datos, n_clusters)
print(clustering$centers)

Plot only variables 1 and 4:

plot(datos[,1], datos[,4], xlab=colnames(datos)[1], ylab=colnames(datos)[4])
for (i in 1:n_clusters) {
  datos_cluster = datos[clustering$cluster==i,]
  color = colors()[i*30]
  lines(datos_cluster[,1], datos_cluster[,4], col=color, xlab="", ylab="", xaxt="n", yaxt="n", xlim=c(4,8), ylim=c(0,4), type="p")
  lines(clustering$centers[i,1], clustering$centers[i,4], col=color, pch=10, type="p", cex=3)
}

3.1.5 Hyperparameters of $k$-means

Main hyperparameters of $k$-means:

Optimal number of clusters $k$
- It depends on the application
- If $k=m$ each data point is a cluster (useless)
- If $k=1$ all data points belong to the same cluster (useless)
Centroid initialization. There are many strategies
- Random initialization may fall far from data or unequally distributed
  - Convergence may be slow
  - Some clusters may remain empty
- Centroids can be chosen among data
  - At least one data instance belongs to every cluster
Every choice of hyperparameters must be run several times, as in all stochastic algorithms
The package kmeans in R automatically repeats the run and selects the best result (parameter nstart)

3.1.6 Validation in unsupervised learning

In unsupervised learning there is no error to validate results
Intra-class variance is a measure of clustering compactness
But intra-class-variance simply decreases with the number of clusters

datos = iris[,1:4]   # Numerical data !!!
errores = vector(length=20)
for (i in 3:20) {
  results = kmeans(datos, i, nstart=10)
  errores[i] = results$tot.withinss
}
plot(3:20, errores[3:20], xlab="k", ylab="error")

Intra-class variance is 0 when each point is a cluster $k=m$
A large number of clusters is not useful

3.1.7 Extrinsic validation

When data include classes, these are not used for clustering
Clustering can be compared to original classes
There is no guarantee that clusters will be in the same order (or even similar) to classes

datos = iris[, 1:4]   # Numerical data !!!
# Clustering
n_clusters = 3
clustering = kmeans(datos, n_clusters)
print(clustering$centers)
# Compute averages of classes (not clusters!)
print("Media setosa")
print(colMeans(iris[iris$Species=="setosa",1:4]))
print("Media versicolor")
print(colMeans(iris[iris$Species=="versicolor",1:4]))
print("Media virginica")
print(colMeans(iris[iris$Species=="virginica",1:4]))
# Plot classes
plot(datos[iris$Species=="setosa", 1], datos[iris$Species=="setosa", 4], col = 30, xlab=colnames(datos)[1], ylab=colnames(datos)[4], xlim=c(4,8), ylim=c(0,4))
lines(datos[iris$Species=="versicolor", 1], datos[iris$Species=="versicolor", 4], col = 60, type="p")
lines(datos[iris$Species=="virginica", 1], datos[iris$Species=="virginica", 4], col = 90, type="p")
# Plot clusters
for (i in 1:n_clusters) {
  color <- colors()[i*30]
  lines(clustering$centers[i,1], clustering$centers[i,4], col=color, pch=10, type="p", cex=3)
}
# Print confusion matrix
clust_fac <- as.factor(clustering$cluster)
print(table(iris$Species, clust_fac))
# factor(clust_fac, levels=rev(levels(clust_fac)))

3.1.8 Other clustering methods

$k$-means is the simplest clustering algorithm
There are many other clustering techniques
- Vector Quantization
- Kohonen’s Self Organizing Maps
- Fuzzy Clustering
- etc.

3.1.9 Exercises

Choose any dataset with numeric variables and apply the k-means algorithm
Set three different numbers of clusters, and check the variance for each value
Discuss which could be a useful number of clusters, in terms of the application

3.2 Dimensionality reduction

In dimensionality reduction

Initial data forms $n\times m$ matrix
The aim is to reduce the number of columns to $k\ll m$
Applications
- Visualization (k=2)
- Sensitivity analysis: determine which features contain important information
- Data compression
- Preprocessing before supervised learning
Theoretical analysis show that data has an intrinsic dimension

Types:

Feature selection: some of the existing columns are used
Feature extraction or projection: new columns are created

Example: data lies on a plane that must be discovered

library(pracma)
library(scatterplot3d)
grid = meshgrid(runif(15), runif(15))
x = matrix(grid$X, 225, 1)
y = matrix(grid$Y, 225, 1)
z = 2*x + 3*y + runif(225)*0.4-0.2
scatterplot3d(x,y,z)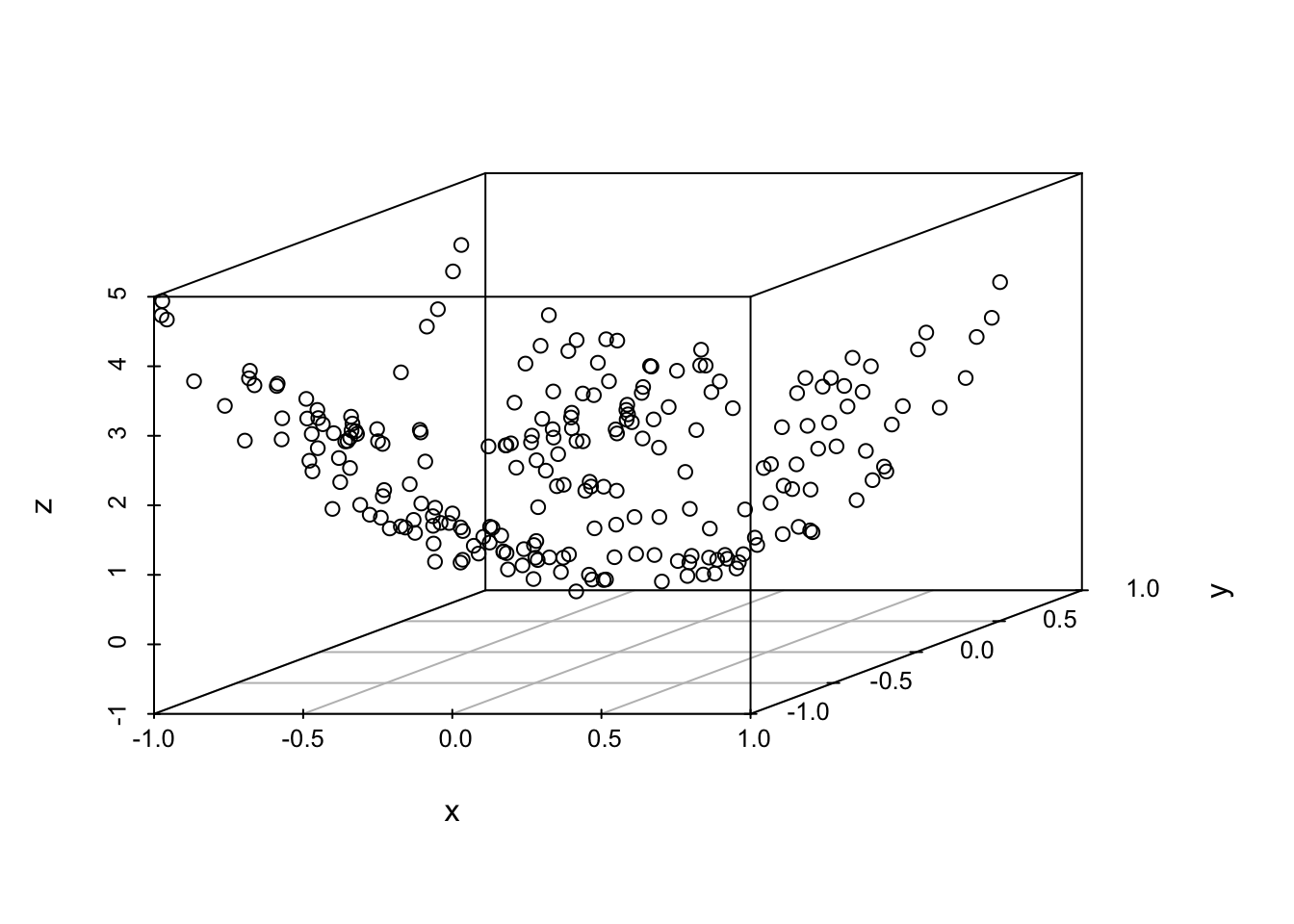

Example: data lies on a nonlinear surface that must be discovered

library(pracma)
library(scatterplot3d)
grid = meshgrid(runif(15)*2-1, runif(15)*2-1)
x = matrix(grid$X, 225, 1)
y = matrix(grid$Y, 225, 1)
z = 2*x^2 + 3*y^2 + runif(225)*0.4-0.2
scatterplot3d(x,y,z)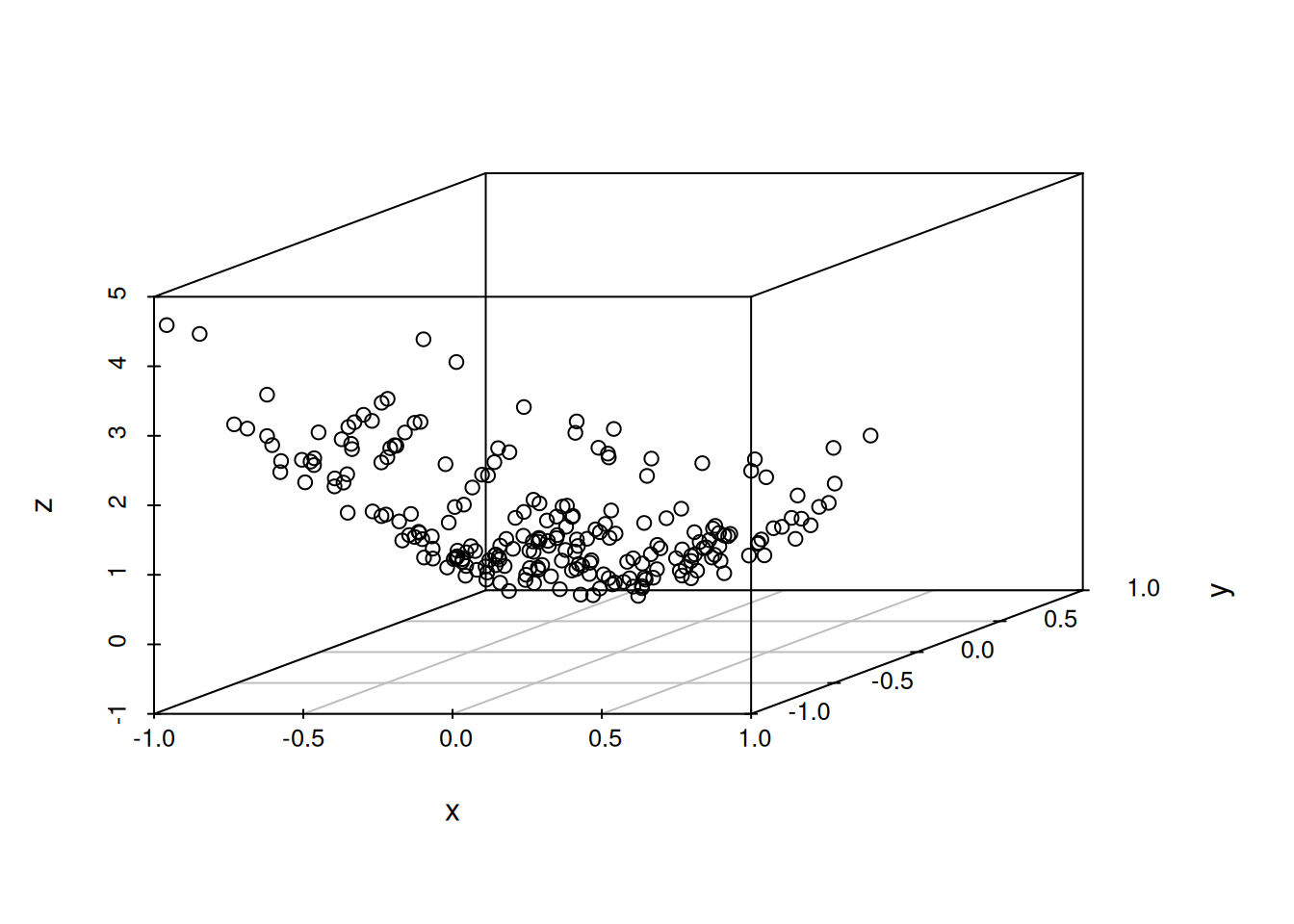

3.2.1 Principal Component Analysis

PCA is a linear transformation of data (orthogonal change of basis)
The new features produced by PCA are:
- Uncorrelated
- Ordered by variance
The algorithm reduces to diagonalization of the covariance matrix
It is critical to center (and scale) data

# First we generate data with very different variances
x = runif(20) * 30 - 15
y = runif(20) * 2 - 1
# After rotation, the high-variance direction cannot be observed
r = as.matrix(cbind(c(1,1), c(1,-1))) / sqrt(2)
girado = as.matrix(cbind(x,y)) %*% r
plot(girado[,1], girado[,2], xlab="", ylab="", asp=1)
components = prcomp(girado, center=TRUE, scale.=TRUE)
# The change of basis is the inverse of the rotation
print(components$rotation %*% r)
# PCA orders the principal components:
lines(c(0, 10), c(0, 10), col="red")
lines(c(0, -1), c(0, 1), col="green")
# Red: first PC
# Green: second PC
print(components$sdev)
summary(components)

3.2.2 Math recall: PCA and Linear Algebra

Start by normalizing data to zero mean:

\[ X_{ij} \leftarrow X_{ij} - \frac{1}{m}\sum_i X_{ij} \]

Data is a $n \times m$ matrix $X$, where the variables are correlated with covariance matrix $C$:

\[ C_{ij} = \frac{1}{n}\sum_k x_{ki} \, x_{kj} \]

Perform orthogonal diagonalization of $C_X=X^\top\,X$:

\[C_X=R\,D\,R^\top\]

This is possible because the $m\times m$ covariance matrix $C_X$ is Symmetric Positive Definite.

Choose the first $k$ Principal Components (PC), where the diagonal matrix $D$ contains the variance of the PCs.

The principal components $Y=X\,R$ are uncorrelated: $C_Y$ is diagonal.

3.2.3 Examples

See the three-dimensional data defined above projected on a plane:

# Data lies on a plane
grid = meshgrid(runif(15), runif(15))
x = matrix(grid$X, 225, 1)
y = matrix(grid$Y, 225, 1)
z = 2*x + 3*y + runif(225)*0.4-0.2
datos = as.data.frame(cbind(x, y, z))
# PCA finds two predominant directions
components = prcomp(datos, center=TRUE, scale.=TRUE)
print(components$sdev)
proy = predict(components, datos)
plot(proy[,1], proy[,2], xlab="", ylab="")
# Notice the different scales in x, y!!
plot(proy[,1], proy[,3], xlab="", ylab="")

Consider again the iris database and use PCA for visualization.

datos = iris[,1:4]
components = prcomp(datos, center=TRUE, scale.=TRUE)
summary(components)
y = predict(components, datos)[, 1:2]
plot(y[iris$Species=="setosa", 1], y[iris$Species=="setosa", 2],
     col="red", pch=17, xlab="", ylab="", xlim=c(-3,3.5), ylim=c(-3,3))
lines(y[iris$Species=="virginica", 1], y[iris$Species=="virginica", 2],
     col="green", pch=16, xlab="", ylab="", type="p")
lines(y[iris$Species=="versicolor", 1], y[iris$Species=="versicolor", 2],
     col="blue", pch=18, xlab="", ylab="", type="p")

We can combine PCA with $k$-means to visualize cluster centres too on the same plane of the two principal components:

n_clusters = 2
clustering = kmeans(datos, n_clusters)
centros = predict(components, clustering$centers)[, 1:2]
plot(y[,1], y[,2])
for (i in 1:n_clusters) {
  datos_cluster = y[clustering$cluster==i,]
  color = colors()[i*30]
  lines(datos_cluster[,1], datos_cluster[,2], col=color, xlab="", ylab="", xaxt="n", yaxt="n", xlim=c(4,8), ylim=c(0,4), type="p")
  lines(centros[i,1], centros[i,2], col=color, pch=10, type="p", cex=3)
}

Dimensionality reduction can be used as a pair encoder/decoder:

datos = iris[,1:4]
components = prcomp(datos, center=TRUE, scale.=FALSE, rank = 2)
medias = matrix(rep(components$center, nrow(components$x)), nrow = nrow(components$x), byrow = T)
encode = predict(components, datos)
base = t(components$rotation)
decode = encode %*% base + medias
n = dim(datos)[1]
m = dim(datos)[2]
sum((datos-decode)^2)/(n*m) # Reconstruction error

3.2.4 Autoencoders

Autoencoders are another method for dimensionality reduction
They are trendy within deep learning models
An autoencoder is a multi-layer neural network
An autoencoder builds a model $y=F(x)$
Each layer builds an internal or hidden model
- Hidden layer: $z_1=F_1(x)$
- Output layer: $y=F_2(z_1)$
The whole NN model is the composition: $F=F_2\circ F_1$
Each internal model may be deep (many layers)
Autoencoders are trained with output=input: $F(x)=x$
Since $F_1$, $F_2$ are inverse, they form an encoder-decoder pair:
- Encoding: $z_1=F_1(x)$
- Decoding: $x_\text{DEC}=F_2(z_1)$
The dimension of the code is the number of neurons in the hidden model (bottleneck)

Many variantes are possible: * Regularization: the code contains mostly zeros (sparse autoencoder) * Learning with noisi instances (denoising autoencoder)

3.2.5 Example

library(autoencoder)
datos = iris[,1:4]
# First repeat PCA
components = prcomp(datos, center=TRUE, scale.=TRUE)
y = predict(components, datos)[, 1:2]
plot(y[, 1], y[, 2])
# Now the autoencoder
datos_m = as.matrix(datos)
# Try first with the default max.iterations = 2000
autoe = autoencode(datos_m, N.hidden = 2, epsilon = 1, lambda = 0, beta = 0, rho = 0.1, rescale.flag = TRUE,max.iterations = 10000)
salida = predict(autoe, datos_m, hidden.output = TRUE)
y_AE = salida$X.output
lines(y_AE[, 1], y_AE[, 2], col="red", type="p")
# Only the first class
plot(y[1:50, 1], y[1:50, 2], xlim=c(-3,3))
lines(y_AE[1:50, 1], y_AE[1:50, 2], col="red", type="p")
# Only the second and third classes
plot(y[51:150, 1], y[51:150, 2], xlim=c(-3,3))
lines(y_AE[51:150, 1], y_AE[51:150, 2], col="red", type="p")

The output (predict) of neural networks is the real output
The output (predict) of an autoencoder is the hidden layer (hidden.output = TRUE)
If we hide the hidden layer (hidden.output = FALSE), we obtain the useless identity function

new_datos = predict(autoe, datos_m, hidden.output = FALSE)
cat("Reconstruction error", new_datos$mean.error, "\n")
cat("First row (data)", datos_m[1, ], "\n")
cat("First row (reconstructed)", new_datos$X.output[1, ], "\n")
# The reconstruction error can be used for anomaly detection
reconstruction_error =rowSums(abs(datos_m - new_datos$X.output))
anomaly = which.max(reconstruction_error)
cat("Error maximum (data)", datos_m[anomaly, ], "\n")
cat("Error maximum (reconstructed)", new_datos$X.output[anomaly, ], "\n")

3.2.6 Exercises

Download a database and perform dimensionality reduction with PCA and an autoencoder
Compare the reconstruction errors

3.3 Time series

3.3.1 Autoregression

In many problems, time is an important variable
In regression, a variable depends on other variables: $y=F(X)$
In autoregression, a variable depends on the same variable at a different time: $ x(t+1) = F(x(t))$
In time series, the state $x(t)$ is a dynamical system

3.3.2 Applications

Translation or filtering: sequence to sequence
Classification: sequence to class
Prediction: sequence to next value

3.3.3 Autoregressive (AR) models

Linear regression on the same (lagged) sequence
Many variants:
- ARMA (moving average)
- ARIMA (integrated)
- ARIMAX (external variables)
- Box-Jenkins

library(forecast)
# Data from http://archive.ics.uci.edu/ml/datasets/Individual+household+electric+power+consumption
household_power_consumption <- read.csv("household_power_consumption.txt", sep=";")
serie <- as.numeric(household_power_consumption$Global_active_power[1:10000])
modelo <- auto.arima(serie)
futuro = predict(modelo, n.ahead = 100)
plot(c(serie[9900:10000], futuro$pred), type="l")

3.3.4 Recurrent neural networks

For training we can use the future values of the series
This backpropagation through time

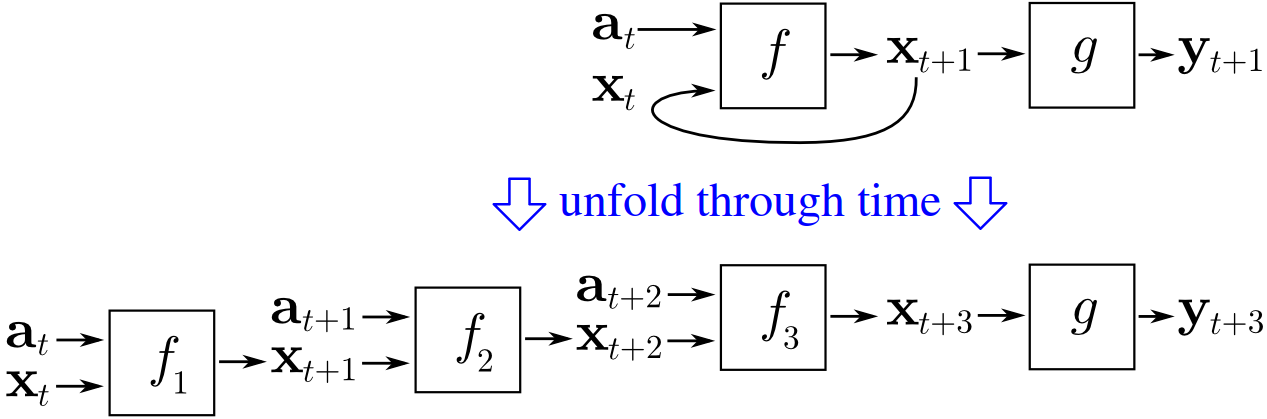
It is equivalent to as many hidden layers as the sequence length
Overfitting analysis is not clear
Gradient vanishing often occurs
In R a recurrent Neural Network is built with the package rnn

library(rnn)
# Data from http://archive.ics.uci.edu/ml/datasets/Individual+household+electric+power+consumption
serie <- as.numeric(household_power_consumption$Global_active_power[1:100])
serie <- serie / max(serie)
n = length(serie)
X = as.matrix(serie[-n])
Y = as.matrix(serie[-1])
network = trainr(Y, X, hidden_dim = 10, learningrate = 0.5, numepochs= 20)
y_pred = predictr(network, X)
plot(as.vector(Y), col='red')
lines(as.vector(y_pred), col='blue')

3.4 Assignment

Clustering

Execute the k-means algorithm on a freely chosen database (it can be the iris database).
Explain the real-world meaning of the clustering task.
Show the effect of extreme values of the number of clusters: Which is the error? Is the result meaningful for the real-world task?

Dimensionality reduction

Execute the PCA algorithm on a freely chosen database (it can be the iris database).
Explain the real-world meaning of the clustering task.
Show how the dimensionality reduction algorithm can be used as an encoder.

Recurrent neural networks

Perform prediction on a freely chosen time series.
Explain the posssible uses of a prediction algorithm for time series.

Machine Learning